Sequences and Series¶
Sequence¶
A sequence is an ordered list of numbers (e.g., 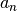 ); the numbers are called
“elements” or “terms”. Every convergent sequence is bounded, thus an unbounded sequence
is divergent.
); the numbers are called
“elements” or “terms”. Every convergent sequence is bounded, thus an unbounded sequence
is divergent.
| Sequence Test | Converge | Notes |
|---|---|---|
| Squeeze Theorem | 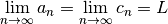 then then 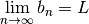 |
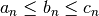 |
| Def 1, pg 692 | 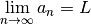 |
|
| l’Hospital’s Rule | 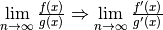 |
where 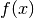 = numerator and = numerator and 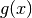 = denominator = denominator |
| Theorem 3, pg 693 | if 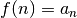 then then 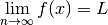 |
|
| Theorem 6, pg 694 | 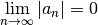 then then 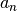 converges converges |
|
| Theorem 9, pg 696 | 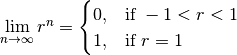 |
Divergent for all other values of  |
| Theorem 12, pg 698 | Every bounded (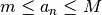 ), monotonic sequence is convergent ), monotonic sequence is convergent |
The bounds exists for 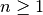 , also see Theorem 10 and 11 , also see Theorem 10 and 11 |
Series¶
A series is the sum of the terms of a sequence: 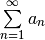 .
.
| Series Test | Converge | Diverge | Notes |
|---|---|---|---|
| Divergence | N/A | 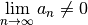 |
Doesn’t show convergence and the converse is not true |
| Integral | if 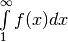 converges converges |
if 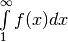 diverges diverges |
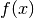 must be positive, decreasing, and continous, also must be positive, decreasing, and continous, also 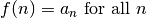 |
| Root | ![\lim\limits_{n\to\infty}\sqrt[n]{|a_n|} = L < 1](../_images/math/4f52b60a094e00049fdd66768ae1f13b2f020804.png) |
![\lim\limits_{n\to\infty}\sqrt[n]{|a_n|} = L > 1 \text{ or } \infty](../_images/math/6c343ef8dba4f21fd734318eff43fa0cb7fd1941.png) |
inconclusive if  |
| Ratio | 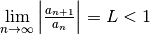 |
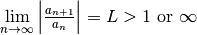 |
inconclusive if 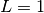 |
| Direct Comparison | 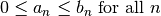 and and 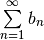 converges converges |
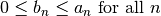 and and 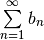 diverges diverges |
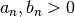 |
| Limit Comparison | 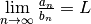 and and 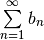 converges converges |
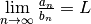 and and 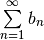 diverges diverges |
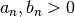 and L is a positive constant, if L is and L is a positive constant, if L is 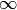 or 0, then pick a different or 0, then pick a different 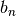 |
| Absolute | 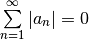 |
Definition of absolutely convergent, the sum is independent of the order in which the terms are summed | |
| Conditional | 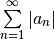 diverges but diverges but 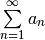 converges converges |
The sum is dependent of the order in which the terms are summed |
Common Series¶
| Series Test | Formula | Converge | Diverge | Notes |
|---|---|---|---|---|
| Alternating | 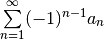 |
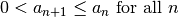 and and 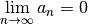 |
N/A | |
| Geometric | 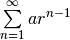 |
 and converges to and converges to 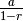 |
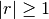 |
finite sum of the first n terms: 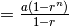 |
| P-Series | 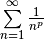 |
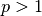 |
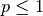 |
cannot calculate sum |
| Power | 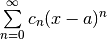 |
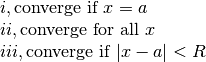 |
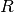 is the radius of convergence, you need to check the end points for convergence too. Typically use Ratio Test. is the radius of convergence, you need to check the end points for convergence too. Typically use Ratio Test. |
|
| Taylor | 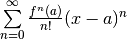 |
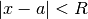 |
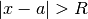 |
Taylor series is centered about a. Same note as power series |
| Maclaurin | 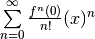 |
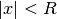 |
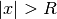 |
A Macluarin series is a Taylor series centered about 0. Same note as power series |